Chess engines act as black boxes: accurate but not interpretable. They output a centipawn evaluation, $s$, and best lines but provide no explicit explanation. This post outlines an approach to explain chess engine evaluations piece by piece.

In particular, we adapt SHAP (a model-agnostic local explainer for tabular data) to chess positions, returning explanations in terms of feature (piece) importance.

@article{lundberg2017unified,
  title={A unified approach to interpreting model predictions},
  author={Lundberg, Scott M and Lee, Su-In},
  journal={Advances in neural information processing systems},
  volume={30},
  year={2017}
}

To use SHAP with chess positions we need to perform three steps:

1. Engines as Classifiers

The centipawn score can be transformed into the probability of victory for White:

This reframes the engine as a binary classifier, making it compatible with SHAP.

2. Pieces as Features

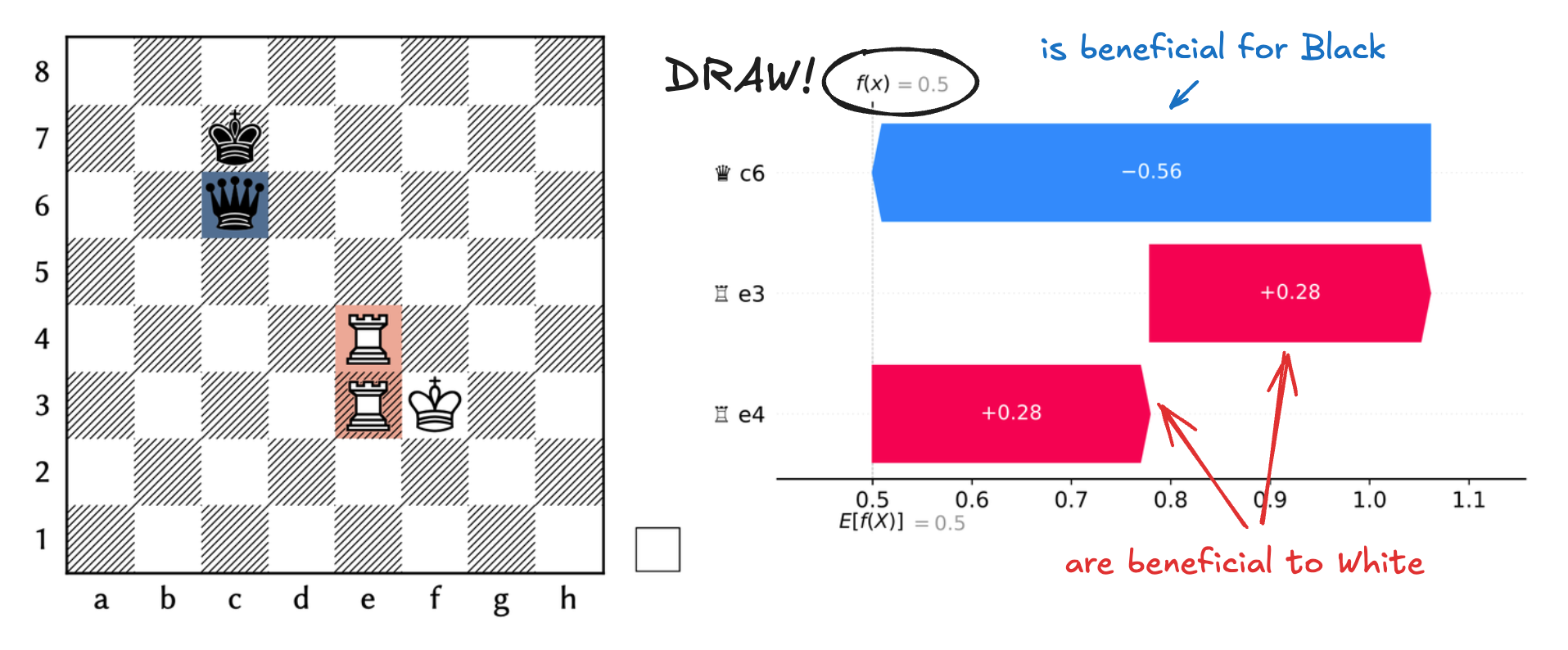
In standard SHAP applications, features are columns of a dataset. Here, the pieces themselves are features (excluding kings). For example, in the position below the features are ${\text{♛ c6}, \text{♖ e4}, \text{♖ e3}}$.

This allows us to attribute contributions to individual pieces.

3. Adapting SHAP

SHAP is based on Shapley values from cooperative game theory. SHAP computes the contribution of a piece by ablating features. For example in the position above, the evaluation with $\text{♖ e3}$ is $50\%$ and drops to $27.7\%$ without, thus:

The contribution of a piece $i$ is the average marginal contribution of piece $i$ across all subsets of other pieces.:

The positions below are all the possible subset of the example position, indicating White - Black probability of winning.

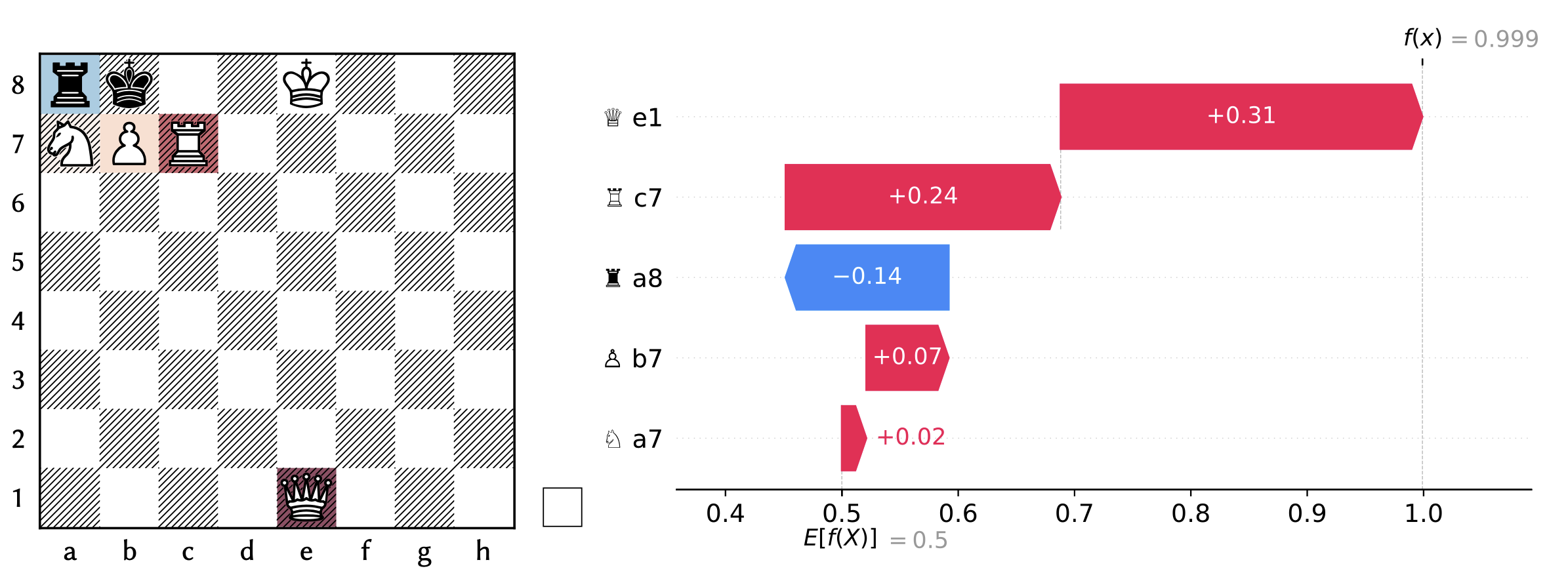
The explanation can be visualized on top of the original board, as well as with the standard SHAP waterfall plot.

Thematic Examples

Here we show some examples of piece-by-piece explanations using SHAP.

Self-blocking Pawn

Q7/3rpkp1/4p1p1/8/2K2P2/5R2/8/6q1 w - - 0 1

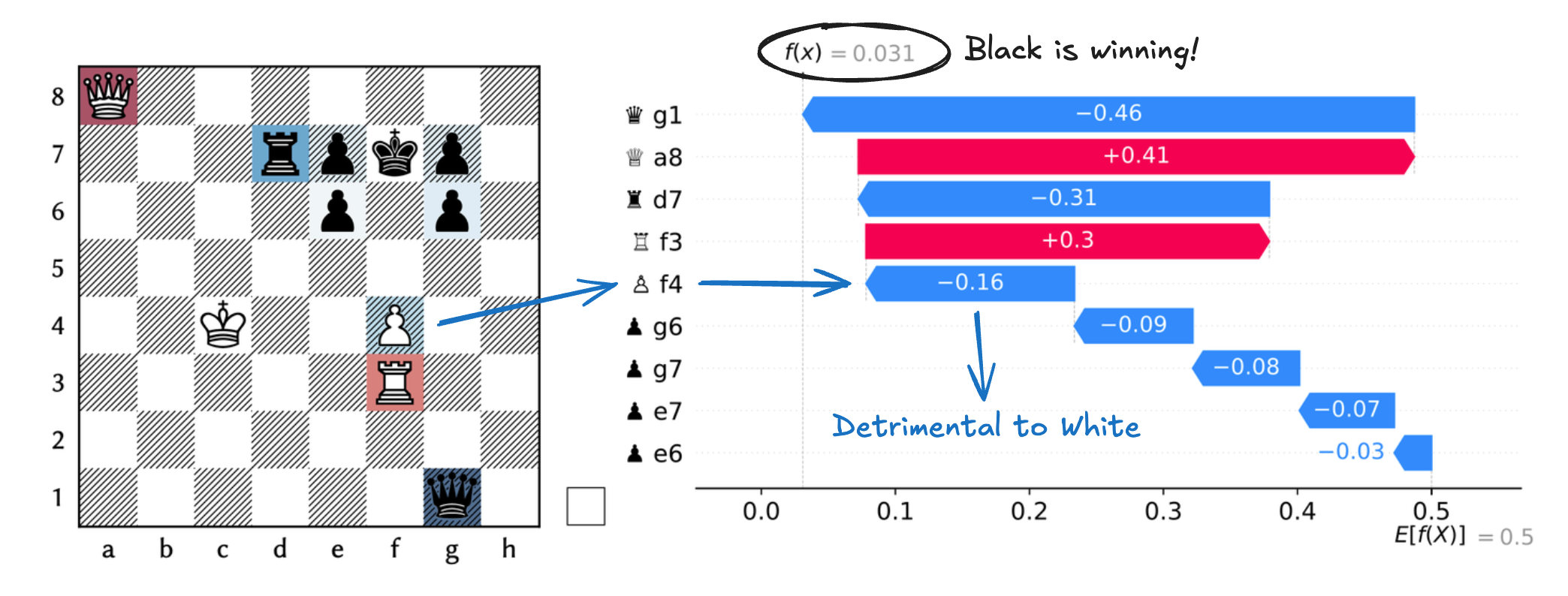
The White pawn blocks its own rook. SHAP assigns the pawn a negative contribution. Indeed, without the pawn on f4, White is checkmating Black.

Bishop vs Knight Endgame

8/3k4/3np2p/p5p1/P5P1/1P2B3/2K4P/8 w - - 0 1

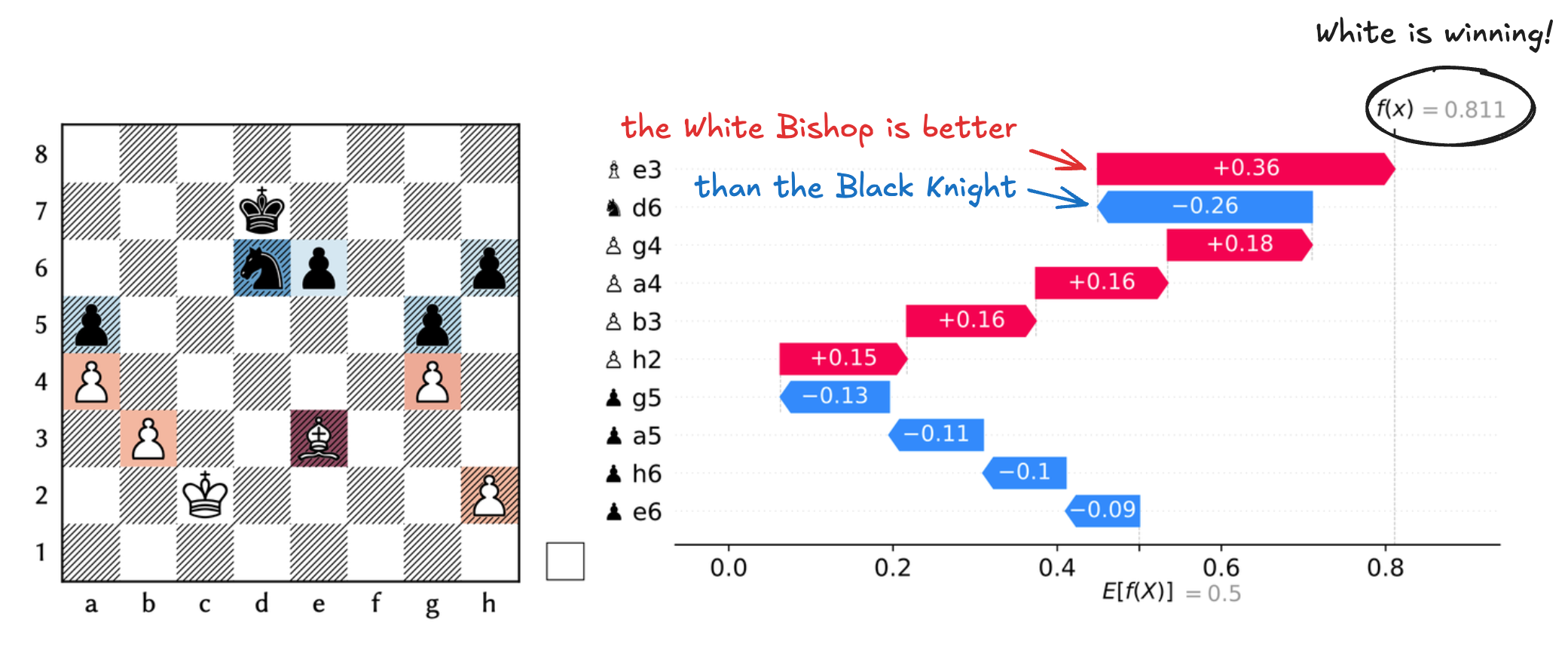
In a classical Bishop vs Knight endgame a key problem is to understand if it is better to have one or the other. In this case the Bishop is better, as the pawn on a5 cannot be defended after 1. Bb6 Nb7 2. Bd4 Nd6 3. Bg7 Nf7 4. Bc3.

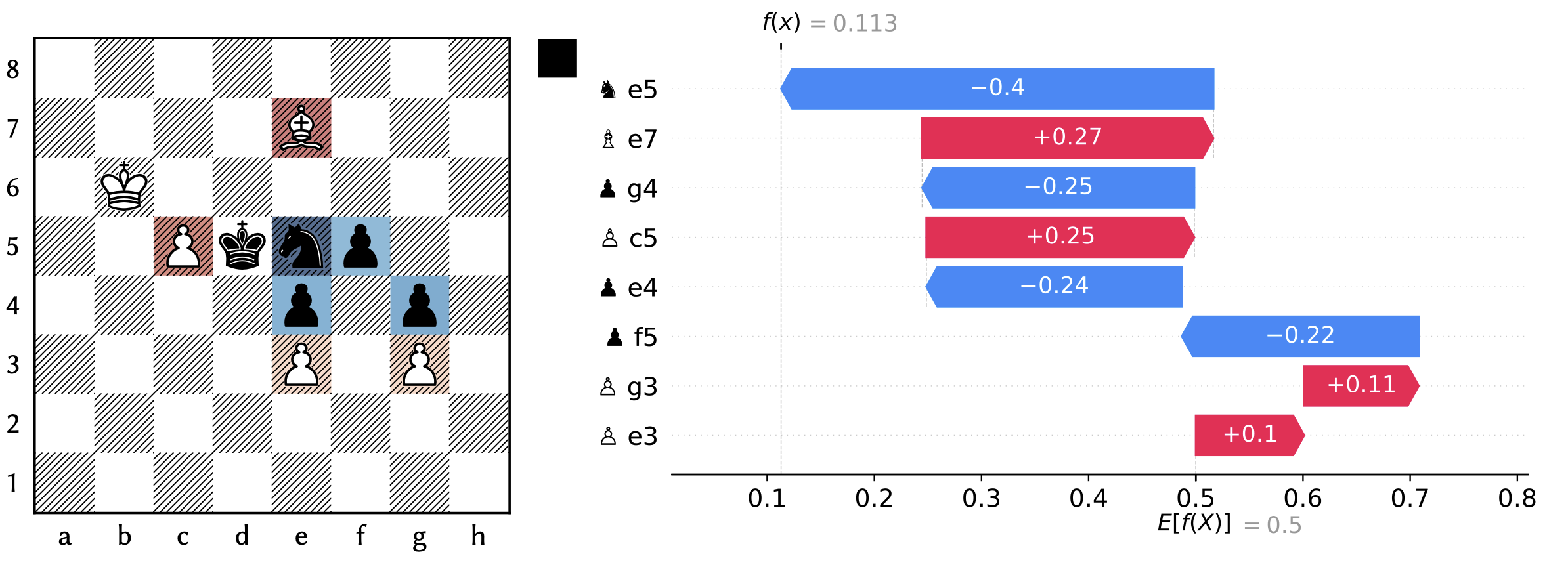
Good Knight, Bad Bishop

8/4B3/1K6/2Pknp2/4p1p1/4P1P1/8/8 b - - 0 133

In this position from Melkumyan–Gabuzyan, ARM-ch rapid, Yerevan 2016, the bishop is instead inferior compared to the knight. The critical move is 133...f4!

Non-contributing Piece

rk2K3/NPR5/8/8/8/8/8/4Q3 w - - 0 1

In this chess puzzle, SHAP suggests that the knight is not contributing to White’s probability of winning. So maybe that’s not the piece you want to move! Try to find the best continuation for checkmate in two moves.

Limitations and Future Work

There are a few limitations to this approach. One of them is that the feature importance is not actionable, it does not tell you what to do, but just give a more didactical assessment of the position. Second, it cannot evaluate the king’s importance, as a position without king is not valid. Finally it is expensive to compute all possible subsets of the position.

Possible future work include ablating coalition of pieces instead of single ones to improve efficiency, compare engines with piece-level attributions and maybe extend this approach to other board games.

You can find the code in the github repo: https://github.com/fspinna/chessplainer, and the full article or arxiv.

@misc{spinnato2025piecebypieceexplanationschesspositions,
      title={Towards Piece-by-Piece Explanations for Chess Positions with SHAP}, 
      author={Francesco Spinnato},
      year={2025},
      eprint={2510.25775},
      archivePrefix={arXiv},
      primaryClass={cs.AI},
      url={https://arxiv.org/abs/2510.25775}, 
}